Exercice 1 : (Vocabulaire des arbres)
https://onecompiler.com/cpp/434ywvv99
exo1-serie4Exercice 2 : (Arbre binaire représenté en tableau)
Soit le tableau suivant qui représente un arbre binaire T en triplets (info, gauche, droit) :
| 23 | 2 | 3 | 5 | 7 | 11 | 13 | 37 | 41 | 19 |
| -1 | 4 | 3 | -1 | -1 | 9 | -1 | 8 | 6 | -1 |
| -1 | 5 | 0 | -1 | -1- | -1 | 2 | 1 | -1 | -1 |
La première colonne (indice 0) représente le nœud dont le champ info est 23 (valeur du nœud), le champ gauche est -1 (indice du fils gauche) et le champ droit est -1 (indice du fils droit), La seconde colonne (indice 1) représente le nœud dont le champ info est 2, le champ gauche est 4 et le champ droit est 5, et ainsi de suite. La valeur (-1) indique l’absence d’un fils gauche ou droit.
- Dessiner l’arbre binaire T et donner sa taille.
- Donner le code C pour représenter l’arbre T de cette manière.
- Écrire une fonction qui détermine la racine de l’arbre T.
- Écrire une procédure qui liste toutes les feuilles de l’arbre T.
- Donner le résultat du parcours de l’arbre T :
I : en ordre infixé,
ii : en ordre préfixé, et
iii : en ordre postfixé.
Solution :
#include <iostream>
using namespace std ;
struct Cell
{
int data ;
int left ;
int right ;
};
typedef struct Cell * ATree ;
int tree_root(ATree atree, int nbre)
{
if(nbre <= 0)
return -1 ;
bool* root_array = new bool[nbre] ;
for(int i = 0; i < nbre ; i++)
root_array[i] = true ;
for(int i = 0; i < nbre ; i++)
{
if(atree[i].left != -1)
root_array[atree[i].left] = false ;
if(atree[i].right != -1)
root_array[atree[i].right] = false ;
}
for(int i = 0; i < nbre ; i++)
if(root_array[i])
return i ;
return -1 ;
}
void tree_leaves(ATree atree, int nbre)
{
for(int i = 0; i < nbre ; i++)
if((atree[i].left == -1)&&(atree[i].right == -1))
cout << "leaf : " << atree[i].data << endl ;
return ;
}
int main()
{
Cell atree[] = { {23, -1, -1}, {2, 4, 5}, {3, 3, 0}, {5, -1, -1}, {7, - 1, -1}, {11, 9, -1}, {13, -1, 2}, {37, 8, 1}, {41, 6, -1}, {19, -1, - 1} } ;
cout << "the root index is : " << tree_root(atree, 10) << endl ;
tree_leaves(atree, 10) ;
return 0 ;
}Exercice 3 : (Implémenter les arbres binaires et leurs fonctions)
Dans un arbre binaire écrire (l’algorithme récursif) :
- une fonction qui calcule le nombre de noeuds.
- une fonction qui fait la somme des valeurs contenues.
- une fonction qui calcule le nombre de feuilles.
- une fonction qui calcule la hauteur.
- tester si un arbre est équilibré.
- fonction de parcours par niveau (en largeur)
Solution :
#include <iostream>
using namespace std ;
/////////// Array tree structure definition ///////////////
struct Cell
{
int data ;
int left ;
int right ;
};
typedef struct Cell * ATree ;
int tree_root(ATree atree, int nbre)
{
if(nbre <= 0)
return -1 ;
bool* root_array = new bool[nbre] ;
for(int i = 0; i < nbre ; i++)
root_array[i] = true ;
for(int i = 0; i < nbre ; i++)
{
if(atree[i].left != -1)
root_array[atree[i].left] = false ;
if(atree[i].right != -1)
root_array[atree[i].right] = false ;
}
for(int i = 0; i < nbre ; i++)
if(root_array[i])
return i ;
return -1 ;
}
/////////// Tree structure definition ///////////////
struct node
{
int data ;
struct node * left ;
struct node * right ;
};
typedef struct node * Tree ;
/////////// Queue structure definition ///////////////
struct element
{
Tree node ;
struct element * next ;
};
typedef struct element * Queue ;
Queue create_queue()
{
return NULL ;
}
bool is_empty_queue(Queue que)
{
if(que == NULL)
return true ;
else
return false ;
}
Queue enqueue(Queue que, Tree node)
{
Queue elm = new element ;
elm->node = node ;
elm->next = NULL ;
if(is_empty_queue(que))
{
que = elm ;
return que ;
}
Queue ptr = que ;
while(ptr->next != NULL)
ptr = ptr->next ;
ptr->next = elm ;
return que ;
}
Queue dequeue(Queue que, Tree &node)
{
if(!is_empty_queue(que))
{
Queue ptr = que ;
node = que->node ;
que = que->next ;
delete ptr ;
return que ;
}
else
{
cout << "Error, the queue is already empty." << endl ;
return NULL ;
}
}
Tree create_tree(ATree atree, int root)
{
if(root == -1)
return NULL ;
Tree ptr = new node ;
ptr->data = atree[root].data ;
ptr->left = create_tree(atree, atree[root].left) ;
ptr->right = create_tree(atree, atree[root].right) ;
return ptr ;
}
void postfix_display(Tree tree)
{
if(tree != NULL)
{
postfix_display(tree->left) ;
postfix_display(tree->right) ;
cout << " " << tree->data ;
}
return ;
}
void prefix_display(Tree tree)
{
if(tree != NULL)
{
cout << " " << tree->data ;
prefix_display(tree->left) ;
prefix_display(tree->right) ;
}
return ;
}
void infix_display(Tree tree)
{
if(tree != NULL)
{
infix_display(tree->left) ;
cout << " " << tree->data ;
infix_display(tree->right) ;
}
return ;
}
int nodes_number(Tree tree)
{
if(tree == NULL)
{
return 0 ;
}
else
{
return 1 + nodes_number(tree->left) + nodes_number(tree->right) ;
}
}
int nodes_sum(Tree tree)
{
if(tree == NULL)
{
return 0 ;
}
else
{
return tree->data + nodes_sum(tree->left) + nodes_sum(tree->right) ;
}
}
int leaves_number(Tree tree)
{
if(tree == NULL)
return 0 ;
if((tree->left == NULL)&&(tree->right == NULL))
{
return 1 ;
}
else
{
return leaves_number(tree->left) + leaves_number(tree->right) ;
}
}
int tree_height(Tree tree)
{
if(tree == NULL)
{
return 0 ;
}
else
{
return 1 + max(tree_height(tree->left), tree_height(tree->right)) ;
}
}
bool balanced_tree(Tree tree)
{
if(tree == NULL)
return true ;
if(abs(tree_height(tree->left) - tree_height(tree->right)) > 1)
return false ;
else
return balanced_tree(tree->left) && balanced_tree(tree->right) ;
}
void by_level_display(Tree tree)
{
Queue que = create_queue() ;
if(tree == NULL)
{
cout << "Tree is empty." << endl ;
return ;
}
que = enqueue(que, tree) ;
while(!is_empty_queue(que))
{
Tree ptr ;
que = dequeue(que, ptr) ;
cout << ptr->data << " " ;
if(ptr->left != NULL)
que = enqueue(que, ptr->left) ;
if(ptr->right != NULL)
que = enqueue(que, ptr->right) ;
}
cout << endl ;
return ;
}
int main()
{
Cell atree[] = { {23, -1, -1}, {2, 4, 5}, {3, 3, 0}, {5, -1, -1}, {7, - 1, -1}, {11, 9, -1}, {13, -1, 2}, {37, 8, 1}, {41, 6, -1}, {19, -1, - 1} } ;
Tree tree = create_tree(atree, tree_root(atree, 10)) ;
postfix_display(tree) ; cout << endl ;
prefix_display(tree) ; cout << endl ;
infix_display(tree) ; cout << endl ;
cout << "The number of nodes on the tree is : " << nodes_number(tree) << endl ;
cout << "The sum of nodes on the tree is : " << nodes_sum(tree) << endl ;
cout << "The number of leaves on the tree is : " << leaves_number(tree) << endl ;
cout << "The height/depth of the tree is : " << tree_height(tree) << endl ;
if(balanced_tree(tree))
cout << "The tree is balanced." << endl ;
else
cout << "The tree is not balanced." << endl ;
by_level_display(tree) ;
return 0 ;
}Exercice 4 : (Évaluation d’expression arithmétique)
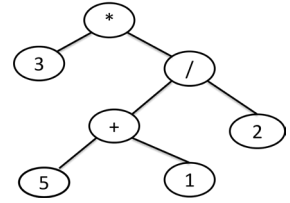
a. Donner une fonction récursive pour évaluer une expression arithmétique sous la forme d’un arbre binaire.
b. Une autre pour imprimer l’expression infixe parenthésée.
Solution :
#include <iostream>
using namespace std ;
struct Node
{
int operand ;
char operation ;
struct Node * left ;
struct Node * right ;
};
typedef struct Node * Tree ;
void postfix_display(Tree tree)
{
if(tree != NULL)
{
postfix_display(tree->left) ;
postfix_display(tree->right) ;
if(tree->operation == '\0')
cout << " " << tree->operand ;
else
cout << " " << tree->operation ;
}
return ;
}
void prefix_display(Tree tree)
{
if(tree != NULL)
{
if(tree->operation == '\0')
cout << " " << tree->operand ;
else
cout << " " << tree->operation ;
prefix_display(tree->left) ;
prefix_display(tree->right) ;
}
return ;
}
void expression_infix_display(Tree tree)
{
if(tree != NULL)
{
if((tree->left == NULL)&&(tree->right == NULL))
{
expression_infix_display(tree->left) ;
cout << tree->operand ;
expression_infix_display(tree->right) ;
}
else
{
cout << '(' ;
expression_infix_display(tree->left) ;
cout << tree->operation ;
expression_infix_display(tree->right) ;
cout << ')' ;
}
}
return ;
}
int expression_evaluation(Tree tree)
{
if((tree->left == NULL)&&(tree->right == NULL))
return tree->operand ;
else
{
switch(tree->operation)
{
case '+' : return expression_evaluation(tree->left) + expression_evaluation(tree->right) ;
case '-' : return expression_evaluation(tree->left) - expression_evaluation(tree->right) ;
case '*' : return expression_evaluation(tree->left) * expression_evaluation(tree->right) ;
case '/' : return expression_evaluation(tree->left) / expression_evaluation(tree->right) ;
}
}
}
int main()
{
Tree n0 = new Node ;
n0->operation = '*' ;
n0->operand = 0 ;
Tree n11 = new Node ;
n11->operation = '\0' ;
n11->operand = 3 ;
Tree n12 = new Node ;
n12->operation = '/' ;
n12->operand = 0 ;
Tree n21 = new Node ;
n21->operation = '+' ;
n21->operand = 0 ;
Tree n22 = new Node ;
n22->operation = '\0' ;
n22->operand = 2 ;
Tree n31 = new Node ;
n31->operation = '\0' ;
n31->operand = 5 ;
Tree n32 = new Node ;
n32->operation = '\0' ;
n32->operand = 1 ;
n0->left = n11 ;
n0->right = n12 ;
n11->left = NULL ;
n11->right = NULL ;
n12->left = n21 ;
n12->right = n22 ;
n21->left = n31 ;
n21->right = n32 ;
n22->left = NULL ;
n22->right = NULL ;
n31->left = NULL ;
n31->right = NULL ;
n32->left = NULL ;
n32->right = NULL ;
postfix_display(n0) ; cout << endl ;
prefix_display(n0) ; cout << endl ;
cout << "3*((5+1)/2) = " << expression_evaluation(n0) << endl ;
expression_infix_display(n0) ;
return 0 ;
}Exercice 5 : (Arbre binaire de recherche)
- Dessiner l’arbre binaire de recherche obtenu en insérant les éléments de la liste suivante dans leur ordre d’arrivée: 30, 40, 23, 58, 48, 26, 11, 13, 20
- Donner le résultat des parcours préfixe, infixe et postfixe de l’arbre précédent
- Donner l’arbre précédent après la suppression des clés suivantes : 48 puis 23.
- Donner l’arbre précédent (avant la suppression) après l’ajout des clés suivantes : 60 puis 17.

