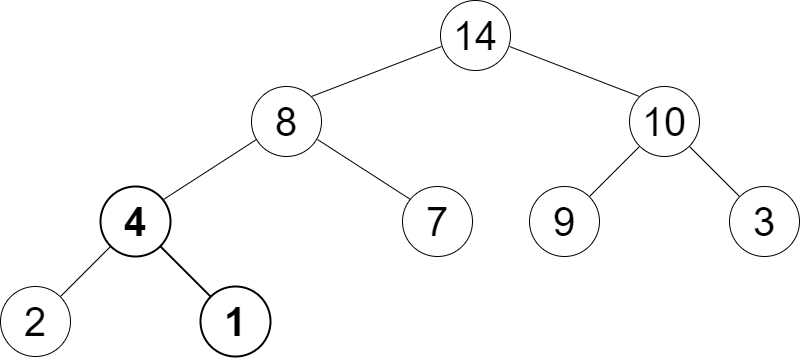
Exercice 1 : (Représentation d’un tas en tableau)
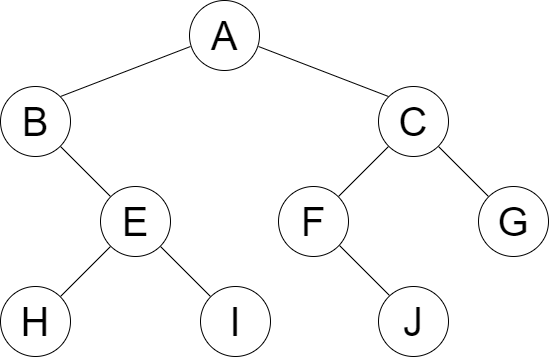
A) Donner la représentation de l’arbre suivant dans un tableau (en suivant les règles de construction d’un tas sous forme de tableau):
Solution :
Les règles pour représenter un tas sous format d’un tableau sont comme suit :
- La racine est à la première position du tableau avec l’indice 1 (le premier indice du tableau n’est pas 0 comme pour le C/C++).
- Chaque fils gauche d’un nœud doit être à la position 2*i de l’indice du père. Par exemple, si le père est à l’indice 3, son fils gauche est à l’indice 6 du tableau.
- Chaque fils droite d’un nœud doit être à la position 2*i+1 de l’indice du père. Par exemple, si le père est à l’indice 3, son fils droite est à l’indice 7 du tableau.
- Si on applique les règles précédentes sur un arbre donné, et on ne trouve pas de case vide dans le tableau, alors l’arbre en question a la structure d’un tas.
A) En appliquant les règles précédentes sur l’arbre, on obtient le tableau suivant :
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| A | B | C | E | F | G | H | I | J |
B) On peut voir que les cases avec l’indice 4, 8,9 et 12 sont vides, donc on peut constater que l’arbre ne peut pas être un tas.
Remarque 1 : Un tas est considéré comme un arbre binaire parfait. Donc par définition, c’est un arbre dans lequel tous les niveaux sont remplis, 1-niveau avec 1 nœud, 2-niveau avec 2 nœuds, 3-niveau avec 4 nœuds, 4-niveau avec 8 nœuds…etc. Sauf, le dernier qui doit seulement être rempli de gauche à droite.
Remarque 2 : Visuellement, il est très facile de distinguer un tas, dans le sens où tous les niveaux sont pleins, il n’y a pas de vide dans les niveaux. Sauf le dernier, qui est rempli de gauche à droite. Pour le transcrire en tableau l’opération est très simple, il suffit d’écrire chaque niveau de l’arbre l’un après l’autre dans le tableau. C’est comme si vous êtes en train de transcrire l’arbre de gauche à droite sur une seule ligne.
Exercice 2 : (Algorithmes et complexité d’un tas)
Avec le TAS max suivant :
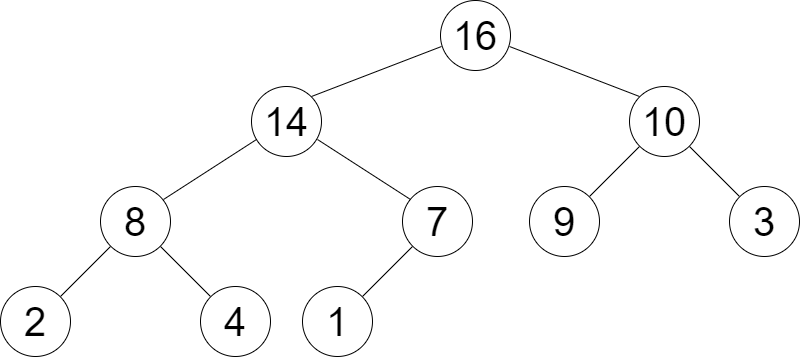
A) Ajouter l’élément de priorité 15 (dessiner tous les arbres intermédiaires jusqu’à l’arbre final)
B) Donner l’algorithme (idée générale ou pseudo-code) d’Ajout/Enfiler d’un élément.
C) Retirer un élément, Suppression/Défiler.
D) Donner l’algorithme (idée générale ou pseudo-code) de retrait d’un élément
E) Estimer la complexité des algorithmes de l’Ajout et la Suppression dans un tas.
F) Déduire la complexité des algorithmes d’Ajout et de Suppression dans une file d’attente (FIFO) avec priorité.
Solution :
Le tas est une structure de données utilisée pour 2 principaux algorithmes : Algorithme de Tri (ce n’est pas le cas pour cet exercice), ou une file (FIFO) à priorité, dans laquelle la valeur maximale est en tête de file lors de l’opération Défiler, pour le tas max. Pour le tas min c’est l’inverse, c’est la valeur minimale qui se trouve en tête de file.
Deux conditions sont nécessaires pour concevoir un tas :
- Le tas doit être un arbre binaire parfait.
- Quelque soit un nœud dans le tas, ses fils doivent obligatoirement être plus petits que leur père, pour le tas max. Et inversement pour le tas min, les fils doivent être plus grands que le père.
A) Ajouter/Enfiler l’élément de priorité 15 dans le tas (qui représente une file à priorité)
Étape 1 : (Insérer l’élément 15 au dernier niveau dans la place vide la plus à gauche)

Étape 2 : (Permuter élément 15 avec son père si l’élément est plus grand que le père)
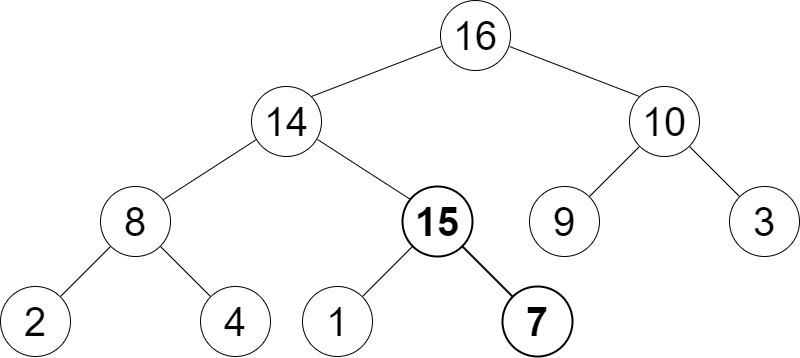
Étape 3 : (Permuter élément 15 avec son père si l’élément est plus grand que le père)
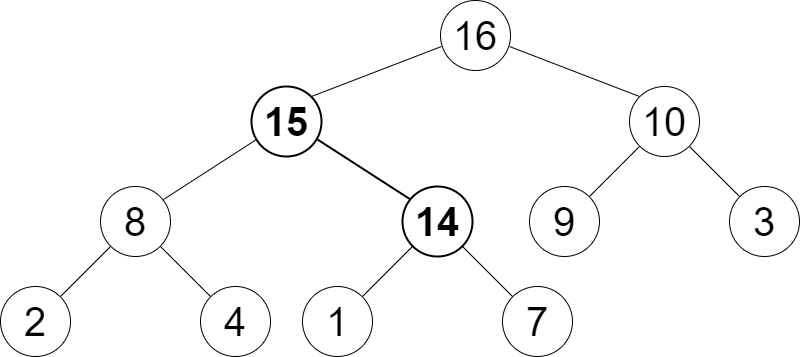
Étape 4 : (S’arrêter si l’élément 15 est inférieur à son père)
B) L’algorithme pour ajouter un élément au tas :
- Créer un nœud et lui donner la valeur à ajouter.
- Insérer le nœud à la dernière position du tas, ça veut dire tout au dernier niveau dans la place vide la plus à gauche.
- Permuter avec la valeur du père tant que le père est inférieur à la valeur insérée pour le tas max. Ou au contraire, tant que le père est supérieur à la valeur insérée pour le tas min.
C) Supprimer/Défiler une valeur du tas (qui représente une file à priorité)
Étape 1 : (accéder/lire la valeur du nœud racine qui représente la tête de file, qui est ici la valeur 16)

Étape 2 : (supprimer la racine et la remplacer par la valeur du dernier nœud du tas. La dernière valeur la plus à gauche au niveau le plus bas, à savoir la valeur 1, sans oublier de la supprimer)

Étape 3 : (Si la valeur du nouveau nœud inséré est supérieur à l’un de ses fils, le permuter avec le fils le plus grand, dans ce cas 14)

Étape 4 : (Si la valeur du nouveau nœud inséré est supérieur à l’un de ses fils, le permuter avec le fils le plus grand, dans ce cas 8)

Étape 5 : (Si la valeur du nouveau nœud inséré est supérieur à l’un de ses fils, le permuter avec le fils le plus grand. C’est le dernier cas puisque le nœud n’a pas de fils supérieur à sa valeur)
D) L’algorithme pour supprimer/défiler un élément du tas (qui représente une file à priorité) est comme suite :
- Lire/accéder à la valeur de la racine du tas, ça représente la tête de la file à priorité, et la valeur la plus grande dans un tas max, ou la plus petite pour un tas min.
- Supprimer la racine et la remplacer par la dernière valeur du tas. C’est la valeur qui se trouve dans le niveau le plus bas du tas, dans la position la plus à droite. Puis de la supprimer aussi.
- Faire la permutation entre le nouveau nœud inséré à la place de la racine, avec le plus grand de ses fils, pour le tas max (le plus petit pour le tas min).
- Répéter l’étape 3 jusqu’à ce qu’aucun des 2 fils du nouveau nœud n’est plus grand que lui, pour le tas max (ou plus petit que lui pour le tas min).
E) La complexité pour supprimer/défiler un élément dans le tas est de O(1). Alors que l’insertion/enfiler d’un nouvel élément est de O(log n). Pour une file à priorité sans utilisation du tas, la suppression est de O(1) lorsque la tête est à l’extrémité des données, et l’insertion est de O(n). C’est pour cette raison que la file à priorité utilisant le tas est préférable à une file à priorité normale.

